En parcourant l’excellent texte d’Ulrich Drepper « What Every Programmer Should Know About Memory » j’ai eu envie de vérifier si j’obtenais expérimentalement des résultats similaires à ceux qu’il présente. J’ai construit une série de petits programmes, qui accèdent de différentes manières à la mémoire et nous présentent des statistiques sur leurs temps d’exécution. Ils sont disponibles dans cette archive.
Le premier programme qui créé une table d’entiers dont la taille N est indiquée en premier argument sur la ligne de commandes. La table est remplie de manière séquentielle, chaque case contient le numéro d’indice de la case suivante.
Nous chronométrons ensuite une série de P parcours de cette table (P étant fourni en second argument sur la ligne de commande) durant lesquels nous consultons simplement le contenu de chaque case. Puis une seconde série de P parcours chronométrés durant lesquels on va modifier la table (un parcours avec incrémentation du contenu de chaque case, suivi d’un parcours avec décrémentation des contenus).
acces-sequentiels-memoire.c :
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <sys/time.h>
int main(int argc, char * argv[])
{
register int i, n;
int nb_entrees;
int nb_parcours;
int * bloc;
struct timeval tv_debut;
struct timeval tv_fin;
long long int duree_lectures;
long long int duree_ecritures;
if ((argc != 3)
|| (sscanf(argv[1], "%d", & nb_entrees) != 1)
|| (sscanf(argv[2], "%d", & nb_parcours) != 1)) {
fprintf(stderr,"usage: %s nb_entrees nb_parcoursn", argv[0]);
exit(EXIT_FAILURE);
}
fprintf(stderr, "Preparation de la table des donnees...n");
bloc = calloc(nb_entrees, sizeof(int));
// Chaque entree contient le numero de la case suivante
for (i = 0; i < nb_entrees-1; i ++)
bloc[i] = i+1;
// La derniere entree est indiquee par -1
bloc[i] = -1;
fprintf(stderr, "Table prete...n");
fprintf(stderr, "Parcours en lecture...n");
gettimeofday(& tv_debut, NULL);
for (n = 0; n < nb_parcours; n ++) {
i = 0;
while(i != -1) {
i=bloc[i];
}
}
gettimeofday(& tv_fin, NULL);
duree_lectures = tv_fin.tv_sec - tv_debut.tv_sec;
duree_lectures *= 1000000;
duree_lectures += tv_fin.tv_usec - tv_debut.tv_usec;
fprintf(stderr, "Parcours en ecriture...n");
gettimeofday(& tv_debut, NULL);
for (n = 0; n < nb_parcours; n ++) {
i = 0;
// On decremente chaque entree sauf la derniere
while(i != -1) {
i=(bloc[i]--);
}
i = 0;
// On incremente chaque entree sauf la derniere
while(i != -1)
i=(++bloc[i]);
}
gettimeofday(& tv_fin, NULL);
duree_ecritures = tv_fin.tv_sec - tv_debut.tv_sec;
duree_ecritures*= 1000000;
duree_ecritures += tv_fin.tv_usec - tv_debut.tv_usec;
duree_ecritures /= 2; // Deux parcours complets
fprintf(stderr, "Parcours termines...n");
// Durees en centiemes de nanosecondes
duree_lectures = duree_lectures * 100000 / (nb_entrees * nb_parcours);
duree_ecritures = duree_ecritures * 100000 / (nb_entrees * nb_parcours);
fprintf(stdout, "Duree par acces lecture : %lld.%lld nsn", duree_lectures/100, duree_lectures%100);
fprintf(stdout, "Duree par acces ecriture : %lld.%lld nsn", duree_ecritures/100, duree_ecritures%100);
return 0;
}
Nous allons tester ce programme avec différentes valeurs de N et P. Pour équilibrer grosso-modo le temps de fonctionnement de l’application, nous allons multiplier N (le nombre de valeurs dans la table) par deux à chaque nouvelle exécution, tandis que nous diviserons P (le nombre parcours) par deux. Pour cela, le petit script suivant nous sera utile :
serie-acces-sequentiels.sh :
#! /bin/sh
FIC_RESULTATS="resultats/sequentiels.txt"
FIC_DATA_READ="resultats/read-sequentiels.txt"
FIC_DATA_WRITE="resultats/write-sequentiels.txt"
FIC_GRAPHIQUE="resultats/graph-sequentiel.gif"
> "$FIC_RESULTATS"
N=1
P=$((512*1024*1024))
taskset -pc 0 $$
while [ "$P" -ge 1 ]
do
echo "$N / $P " >&2
echo "taille bloc : $N, nb_cycles : $P" >> "$FIC_RESULTATS"
./acces-sequentiels-memoire "$N" "$P" >> "$FIC_RESULTATS"
N=$((N<<1))
P=$((P>>1))
done
grep ecriture < "$FIC_RESULTATS" | awk '{print $6}' > "$FIC_DATA_WRITE"
grep lecture < "$FIC_RESULTATS" | awk '{print $6}' > "$FIC_DATA_READ"
echo "set terminal gif giant size 1600,1200; set output '$FIC_GRAPHIQUE'; set multiplot layout 2,1; "
"set xlabel 'log2(nombre de blocs)'; set ylabel 'duree boucle (ns)'; "
"plot '$FIC_DATA_WRITE' with line lc rgb '#FF0000'; "
"replot '$FIC_DATA_READ' with line lc rgb '#0000FF';"
| gnuplot
Pour éviter toute migration intempestive du processus, on le fixe (avec taskset) sur le processeur 0.
On remarquera l’initialisation des variables N et P : nous allons commencer par un bloc de 1 entier, accédé 512 millions de fois, pour terminer par un bloc de 512 millions d’entrées entières (occupant donc 2Go) accédé une seule fois. On peut naturellement jouer sur ces valeurs en fonction de la taille mémoire et de la vitesse de traitement du système. On notera également que les dernières lignes du script invoquent l’utilitaire gnuplot pour créer un fichier graphique avec les résultats.
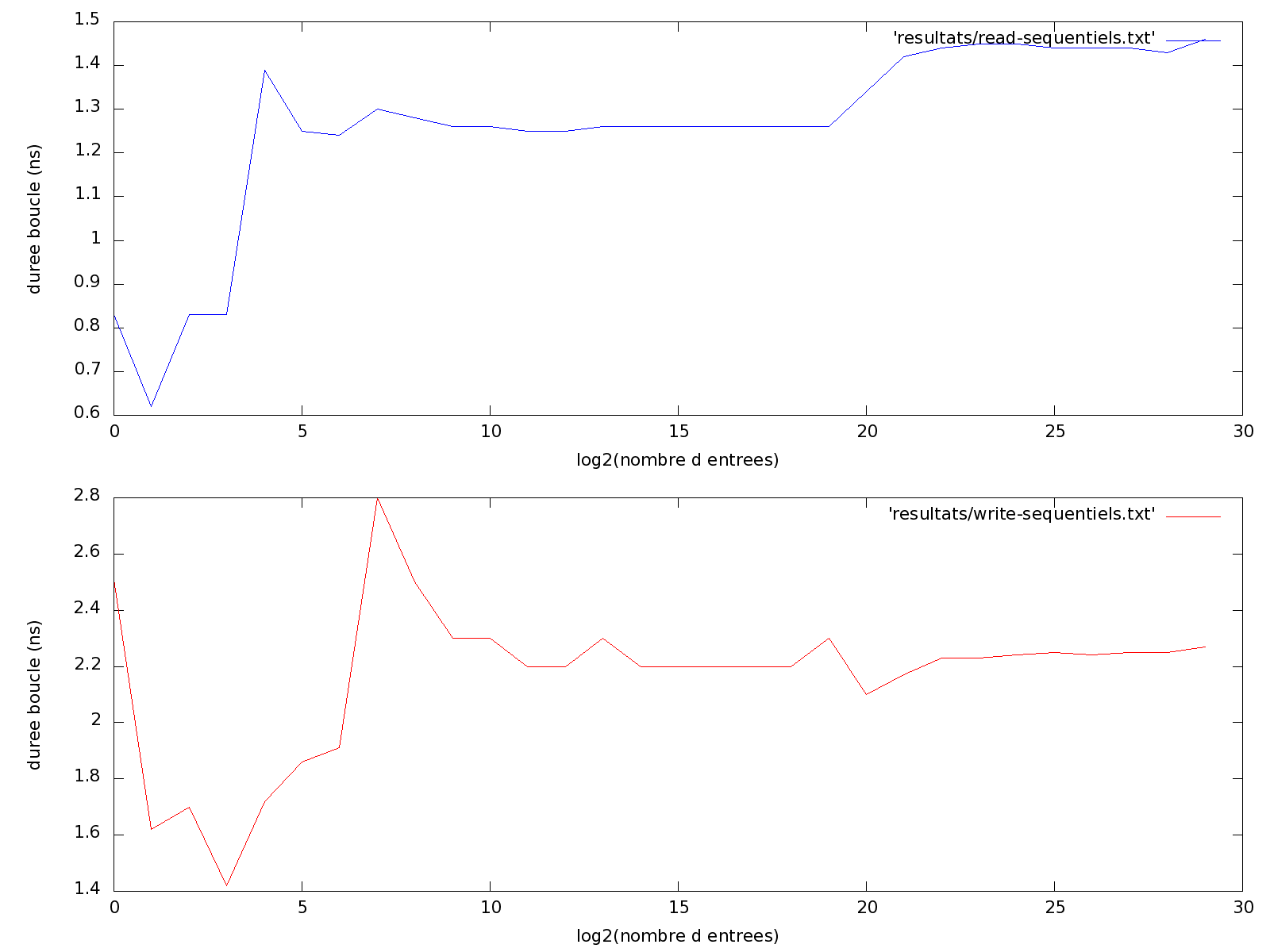
Voici une première exécution :
$ ./series-acces-sequentiels.sh pid 6971's current affinity list: 0-3 pid 6971's new affinity list: 0 1 / 536870912 Preparation de la table des donnees... Table prete... Parcours en lecture... Parcours en ecriture... Parcours termines... 2 / 268435456 [...] 536870912 / 1 Preparation de la table des donnees... Table prete... Parcours en lecture... Parcours en ecriture... Parcours termines... $
Et le résultat se présente sur les figures suivantes :
Pour pouvoir comprendre l’intérêt de ce graphique, il nous faut le comparer à un autre type d’accès mémoire : l’accès aléatoire. Nous reprenons notre programme précédent en modifiant simplement l’initialisation du bloc : chaque case va contenir le numéro d’indice d’une autre case du tableau choisie aléatoirement. Pour s’assurer que nous ayons un parcours complet du tableau en N étapes, lorsque nous déterminons le numéro d’indice de la case visée, nous nous assurons que cette dernière soit vide (sinon on prend la suivante dans le tableau et on recommence la vérification).
acces-aleatoires-memoire.c :
[...]
// On alloue une table de N entrees, initialisees a -1
bloc = calloc(nb_entrees, sizeof(int));
for (i = 0; i < nb_entrees; i ++)
bloc[i] = -1;
n = 0;
i = 0;
// Remplir N-1 entrees (la derniere sert d'arret)
while (n < nb_entrees-1) {
// Remplir de maniere aleatoire avec le numero
// d'une autre entree actuellement vide.
bloc[i] = rand() % nb_entrees;
// Si elle n'est pas vide, rechercher la premiere
// entree vide a la suite.
while (bloc[bloc[i]] != -1) {
bloc[i] ++;
if (bloc[i] == nb_entrees)
bloc[i] = 0;
}
i = bloc[i];
n++;
}
// La derniere entree contient toujours -1
[...]
Bien sûr, un script nommé series-acces-aleatoires.sh permet d’exécuter ce programme avec les mêmes arguments que précédemment. Le temps d’exécution du script est nettement plus long, ne serait-ce qu’à cause de l’initialisation des tables qui demandent des calculs importants pour l’obtention des valeurs aléatoires.
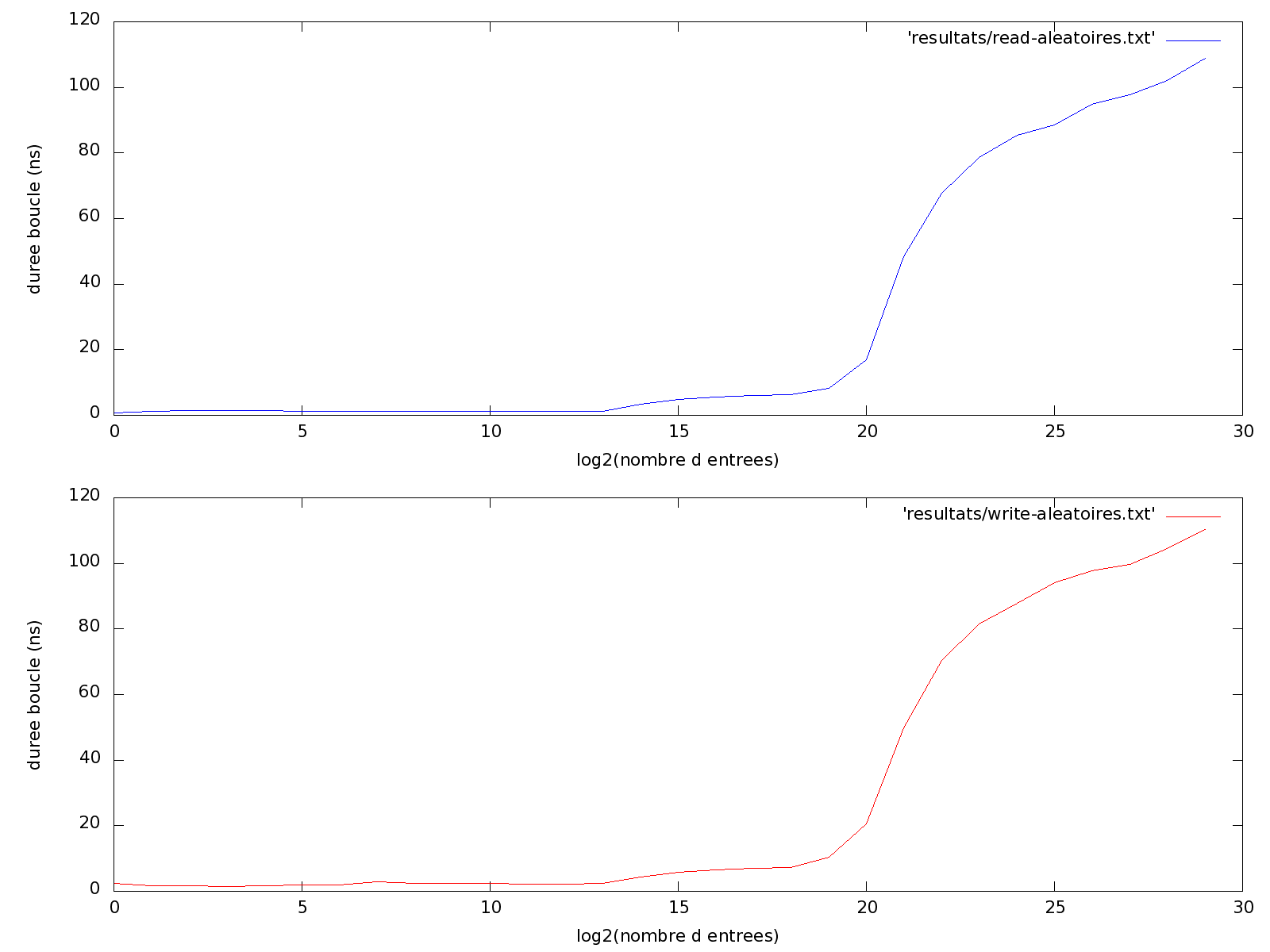
$ ./series-acces-aleatoires.sh pid 8003's current affinity list: 0-3 pid 8003's new affinity list: 0 1 / 536870912 Preparation de la table des donnees... Table prete... Parcours en lecture... Parcours en ecriture... Parcours termines... 2 / 268435456 [...] $
Voici le graphique correspondant à cette exécution.
Nous pouvons remarquer que le temps d’accès, en opérant de manière aléatoire sur les données, est sensiblement plus long dès que l’on dépasse une table de 2^13 entiers. Cette valeur correspond à 8192 entiers, soient 32Ko ce qui représente la taille du cache de premier niveau (L1d). Tant que les données manipulées arrivent à tenir dans ce cache, le mode de parcours importe peu, nous avons un comportement optimal pour l’accès aux données mémoire.
Une fois que l’on dépasse le cache L1, les parcours aléatoires nécessitent de charger fréquemment des lignes de mémoire depuis le cache L2, avec un temps d’accès un peu plus long. Les parcours séquentiels ne présentent pas beaucoup de différences d’exécution car le processeur utilise une « fenêtre » mémoire de la taille de L1 qu’il déplace sur l’ensemble des données.
Ensuite, nous remarquons à nouveau une envolée des temps d’accès aléatoire à partir de 2^19 entiers, soient 2 Mo de données. Cette fois c’est le cache de second niveau qui est débordé. Celui-ci contient environ 4Mo de données, mais il est partagé entre les différents cœurs du processeur et dès que le jeu de données manipulé dépasse 2Mo environ, le processeur doit aller chercher ses informations dans la mémoire dynamique du système, dont l’accès est beaucoup plus long que celui de la mémoire statique du cache.
Ces expériences nous montrent bien que l’utilisation d’ensembles de travail de tailles inférieures à 32 Ko est optimale, qu’une première dégradation intervient lorsqu’on dépasse cette limite sauf si les accès mémoire se font de manière très localisée (comparable à nos parcours séquentiels). Au-delà de 4Mo de données, les performances s’effondreront si nous ne sommes pas capables – en organisant et en structurant correctement nos variables – de garantir des accès les plus localisés aux données. Bien sûr ces valeurs dépendent du processeur et de son niveau de cache. Rappelons que le nom et le type de processeur sont visibles avec une commande :
$ cat /proc/cpuinfo
Les informations techniques sur le cache d’un processeur donné se trouvent assez facilement sur le site de son fabricant ou sur Wikipedia.
Bonjour,
je n’ai pas très bien compris le choix de P=512*1024*1024.
Svenk.